熵
参考:https://zh.wikipedia.org/wiki/熵_(信息论\
在信息论中熵(entropy)是接收的每条消息中包含的信息的平均量,又被称为信息熵、信源熵、平均自信息量。
熵也可以理解为不确定性的量度,因为越随机的信源的熵越大。这里的想法是,比较不可能发生的事情,当它发生了,会提供更多的信息。
如果有一个系统S内存在多个事件S={E1,E2,...,En},每个事件的概率分布P={p1,p2,...,pn},则每个事件本身的讯息(自信息)为:
Ie=−log2pi(对数以2为底,单位是比特(bit))
Ie=−lnpi(对数以e为底,单位是纳特/nats)
如英语有26个字母,假如每个字母在文章中出现次数平均的话,每个字母的信息量为:
Ie=−log2261=4.7
而汉字常用的有2500个,假如每个汉字在文章中出现次数平均的话,每个汉字的信息量为:
Ie=−log225001=11.3
实际上每个字母和每个汉字在文章中出现的次数并不平均,比方说较少见字母(如z)和罕用汉字就具有相对高的信息量。但上述计算提供了以下概念:使用书写单元越多的文字,每个单元所包含的讯息量越大。
熵是整个系统的平均信息量:
Hs=−i=1∑npilog2pi
若pi=0,则定义0log0=0。通常对数以2为底或以e为底,这时熵的单位分别作为比特(bit)或奈特(nat)。
熵越大,随机变量的不确定性越大。
极值性
当所有事件有相同机会出现的情况下,熵达到最大值(所有可能的事件同等概率时不确定性最高)
0⩽Hn(p1,p2,...,pn)⩽Hn(n1,n1,...,n1)=logn
举例来说,当随机变量只取两个值时,例如1和0,则随机变量X的分布为
P(X=1)=p,P(X=0)=1−p,0⩽p⩽1
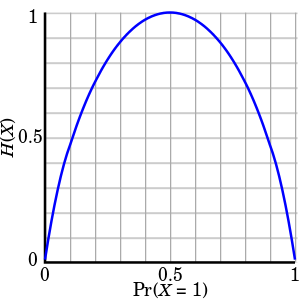
熵为H(p)=−plog2p−(1−p)log2(1−p)
这时熵随着概率p变化的曲线如图,当p=0.5时熵取值最大,系统的不确定性最大。