k近邻模型

$k$近邻（k-Nearest Neighbor，简称kNN）学习是一种常用的监督式学习方法，其工作机制非常简单：

给定测试样本，基于某种距离度量找出训练集中与其最靠近的$k$个训练样本，然后基于这$k$个“邻居”的信息来进行预测。通常，在分类任务中可使用“投票法”，即选择这$k$个样本中出现最多的类别标记作为预测结果；在回归任务中可以使用“平均法”，即将这$k$个样本的实值输出标记的平均值作为预测结果；还可以基于距离远近进行加权平均或加权投票，距离越近的样本权重越大。

$k$近邻有个明显的不同之处：它似乎没有显示的训练过程。事实上，它是“懒惰学习”（lazy learning）的著名代表，此类学习技术在训练阶段仅仅是把样本保存起来，训练时间开销为0，待收到测试样本后再进行处理，这种称为“急切学习”。

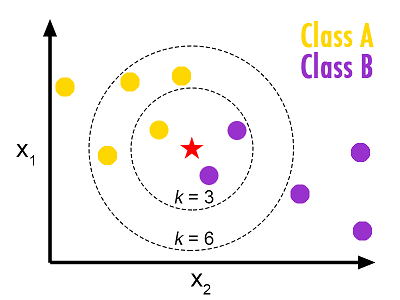
pic source： https://helloacm.com/a-short-introduction-to-k-nearest-neighbors-algorithm/

1.距离度量

特征空间中两个实例点的距离是两个实例点的相似度的反映。$k$近邻模型的特征空间一般是$n$维实数向量空间$R^n$。使用的距离是欧式距离，但也可以使其他距离，比如更一般的$L_p$距离（$L_p$ distance），或Minkowski距离。

设特征空间$X$是$n$维实数向量空间$R^n$，$x^{(i)},x^{(j)}\in X$，$x=(x_0, x_1, x_2, ..., x_n)^T$，$x^{(i)},x^{(j)}$的$L_p$距离定义为：

$L_p(x^{(i)},x^{(j)})=\big( \displaystyle\sum_{k=1}^n|x^{(i)}_k-x^{(j)}_k|^p\big)^{\frac{1}{p}}$

这里$p \geqslant 1$。当$p=2$时，称为欧式距离（Euclidean distance），即

$L_2(x^{(i)},x^{(j)})=\big( \displaystyle\sum_{k=1}^n|x^{(i)}_k-x^{(j)}_k|^2\big)^{\frac{1}{2}}$

当$p=1$时，称为曼哈顿距离（Manhanttan distance），即

$L_1(x^{(i)},x^{(j)})=\displaystyle\sum_{k=1}^n|x^{(i)}_k-x^{(j)}_k|$

当$p=\infty$时，它是各个坐标距离的最大值，即：

$L_\infty(x^{(i)},x^{(j)})=\max_k|x^{(i)}_k-x^{(j)}_k|$

下图给出了$p$取不同值时，与原点的$L_p$距离为$1$（$L_p=1$）的图形。

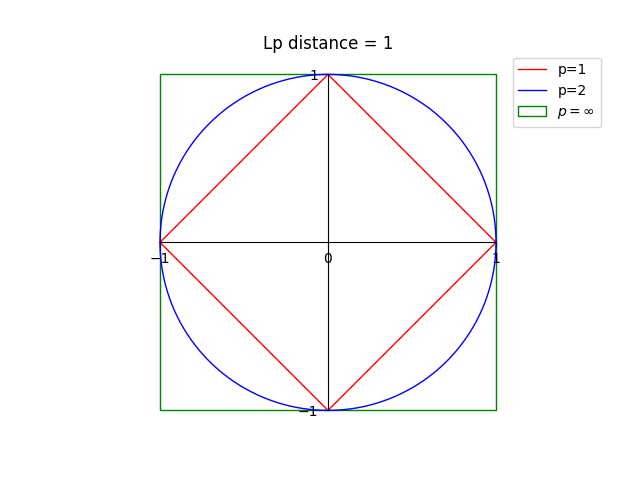
2. k近邻算法

输入：训练集

$T=\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})\}$

其中$x^{(i)}\in X= R^n$为实例的特征向量，$y^{(i)}\in Y=\{c_1, c_2, ...,c_t\}$为实例的类别，$i=1,2,...,m$。某个实例特征向量$x$。

输出：实例$x$的所属类别$y$

1）根据给定的距离度量，在训练集$T$中找出与$x$最邻近的$k$个点，涵盖这$k$个点的邻域记作$N_k (x)$；

2）在$N_k (x)$中根据分类决策规则（如多数表决）决定$x$的类别：

$y=arg \max_{c_j} \displaystyle\sum_{x_i\in N_k (x)} I(y_i=c_j)$

其中$i=1,2,...,m$，$j=1,2,...,t$，$I$为指示函数，即当$y_i=c_j$时为$1$，否则为$0$。

$k$近邻的特殊情况是$k=1$的情形，称为最近邻算法。对于输入的实例点$x$，最近邻算法将训练数据集中与$x$最近的类作为$x$的类。

$k$值的选择会对$k$近邻法的结果产生重大影响。

如果选择较小的$k$值，“学习”的估计误差（estmation error）会增大，预测的结果会对近邻的节点比较敏感。

如果寻则较大的$k$值，“学习”的近似误差（approximation error）会增大，与输入实例较远的训练实例也会对预测起作用，使预测发生错误。

实际中，$k$一般取一个比较小的数值，并采用交叉验证法来选取最优的$k$值。

k近邻法最简单的办法就是线性扫描（linear scan），这时要计算输入实例和每一个训练实例的距离，当训练集很大时，非常耗时，这种方法不可行。

下面介绍$kd$树（$kd$ tree）方法。