向量内积

在数学中，点积（Dot Product）又称数量积，是一个接受两个等长度的数字序列（通常是向量坐标），然后返回单个数字的代数运算。在欧几里德几何中，两个笛卡尔坐标向量的点积常称为内积（Inner Product）。

从代数的角度看，先对两个数字序列中的每组对应元素求积，再对所有积求和，结果即为点积。

从几何角度看，点积则是两个向量的长度与它们的夹角的余弦的积。

代数定义：

两个向量 $\vec{a}=[a_1, a_2, ..., a_n]$ 和 $\vec{b}=[b_1, b_2, ..., b_n]$ 的点积定义为：

$\vec{a} \cdot \vec{b} = \displaystyle\sum_{i=1}^n a_ib_i= a_1b_1+a_2b_2+...+ a_nb_n$

几何定义：

在欧几里德空间中，点积可以直观的定义为：

$\vec{a} \cdot \vec{b} =|{a}||{b} | \mathrm{cos}\theta$

这里$|\vec{x}|$表示向量$\vec{x}$的模的长度，$\theta$表示两个向量的角度。

当两个向量互相垂直时点积总是为零。因为$\mathrm{cos} 90 = 0$。当两个向量方向相同时，角度为$0$，内积为正的最大；当两个向量方向相反时，角度为$180$，内积为负的最大。

若${a}$和${b}$都是单位向量（长度为1），它们的点积就是它们的夹角的余弦。那么给定两个向量，它们之间的夹角可以通过下列公式得到：

$\mathrm{cos} \theta =\frac{ \vec{a} \cdot \vec{b} }{ |{a}| |{b}|}$

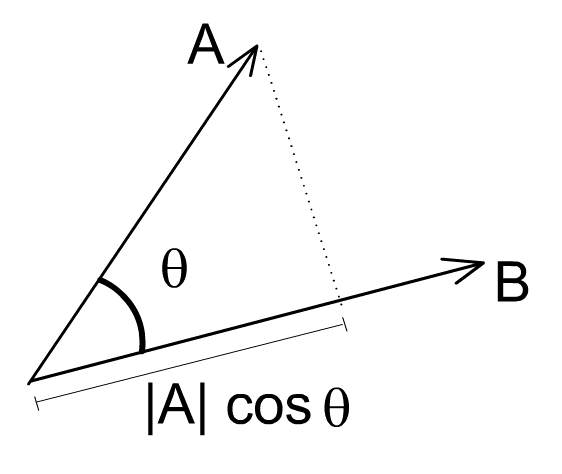
向量的内积可以理解为向量A在向量B上的投影跟向量B的长度的乘积。

source: https://zh.wikipedia.org/wiki/点积