kd树方法

$kd$树是一种对$k$维空间中的实例点进行存储以便对其进行快速检索的树形结构。它是二叉树，表示对$k$维空间的一个划分（partition）。构造$kd$树相当于不断地用垂直于坐标轴的超平面将$k$维空间划分，构成一列的$k$维超矩形区域。$kd$树的每个节点对应于一个$k$维超矩形区域。

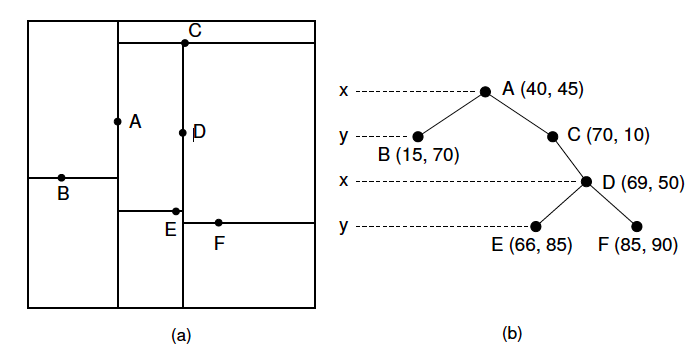
pic source: http://homes.sice.indiana.edu/yye/lab/teaching/spring2014-C343/moretrees.php

1. 构造平衡$kd$树算法

输入：$k$维空间数据集$T=\{x^{(1)},x^{(2)},...,x^{(m)}\}$，其中$x^{(i)}=(x_1, x_2, ..., x_k)^T$，$i=1,2,...,m$

输出：kd树

1）开始：构造根节点，根节点对应于包含$T$的$k$维空间的超矩形区域。

选择$x_1$为坐标轴，以$T$中所有实例的$x_1$坐标的中位数为切分点，将根节点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴$x_1$垂直的超平面实现。

由根节点生成深度为1的左右子树：左子树对应于坐标$x_1$的值小于切分点的子区域，右子树对应于坐标$x_1$的值大于切分点的子区域。

将落在切分超平面上的实例点保存在根节点。

2）重复：对于深度为$l$的节点，选择$x_j$为切分的坐标轴，$j=l\pmod k+1$，举例来讲就是第一次切分选择坐标$x_1$，第二次选择坐标$x_2$，第三次选择坐标$x_3$，当$k$维后，返回到$x_1$继续作为切分坐标。切分由通过切分点并与轴$x_j$垂直的超平面实现。

对于左右子树，以$x_j$坐标的中位数为切分点，并保存为子树的根节点，然后同样分成两个子树。

3）直到两个子区域没有实例存在时停止，从而形成$kd$树的区域划分。

2. kd树的最近邻搜索

输入：已经构造好的$kd$树；目标点$x$

输出：$x$的最近邻

1）首先在$kd$树中找出包含目标点$x$的叶节点。方法是从根节点出发，递归地向下访问$kd$树，若目标点$x$当前维的坐标小于切分点的坐标，则往左子树查找，否则往右子树查找，一直到叶节点为止。

2）以此叶节点为“当前最邻近点”

3）递归往上回退，在每个节点上进行如下操作

• 如果该节点的实例比当前保存的最近点的距离更近，则以该节点为“当前最邻近点”
• 检查另一边子树有没有更近的点，如果有则从该节点往下找
• 即检查当前节点的超平面是否跟以目标节点$x$为圆心，目标节点$x$与“当前最邻近点”的距离为半径构成的圆体相交。
• 如果相交，可能在超平面的另外一侧有节点离目标节点更近，因此移动到超平面的另外一侧的递归执行搜索
• 如果不相交，则向上回退

4）当回退到根节点时（根节点已经完成了步骤3 的操作），搜索结束，最后的“当前最近点”即为$x$的最邻近点。

如果实例点是随机分布的，则$kd$树搜索的平均计算复杂度是$O(logN)$。$kd$树更适用于训练实例数远大于空间维数的情况，如果训练实例数接近空间维数，则效率退化为线性扫描。

3. 例子

示例1：

pic source: http://blog.csdn.net/baimafujinji/article/details/52928203

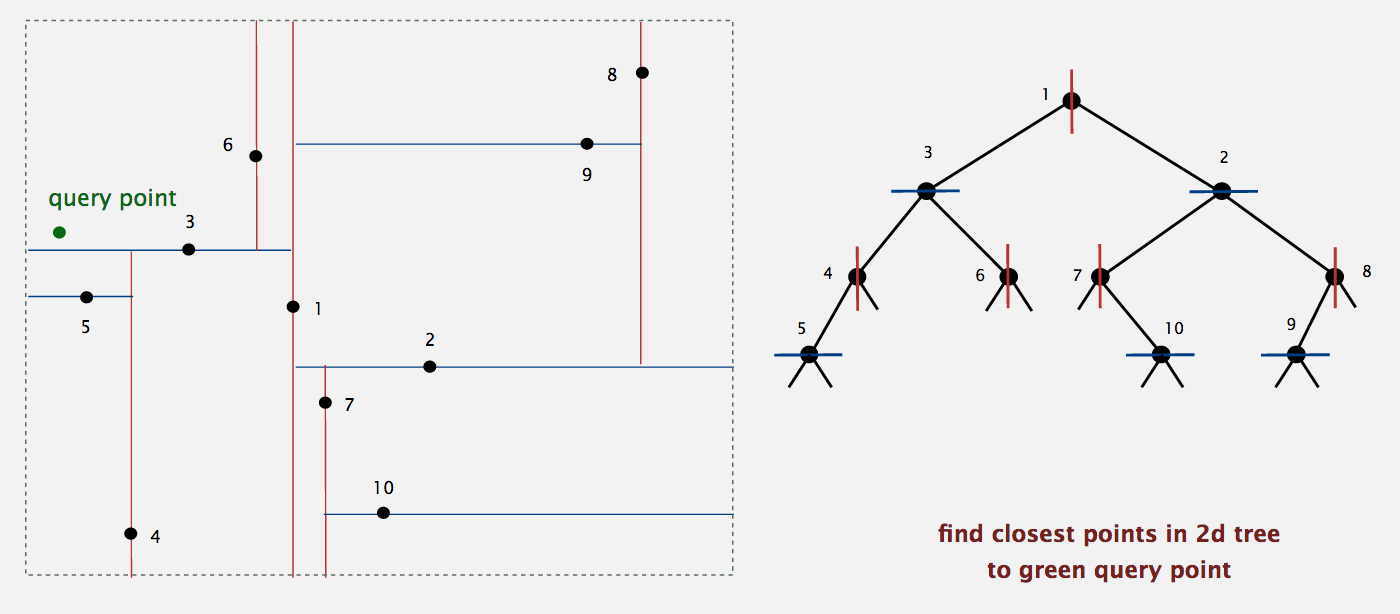
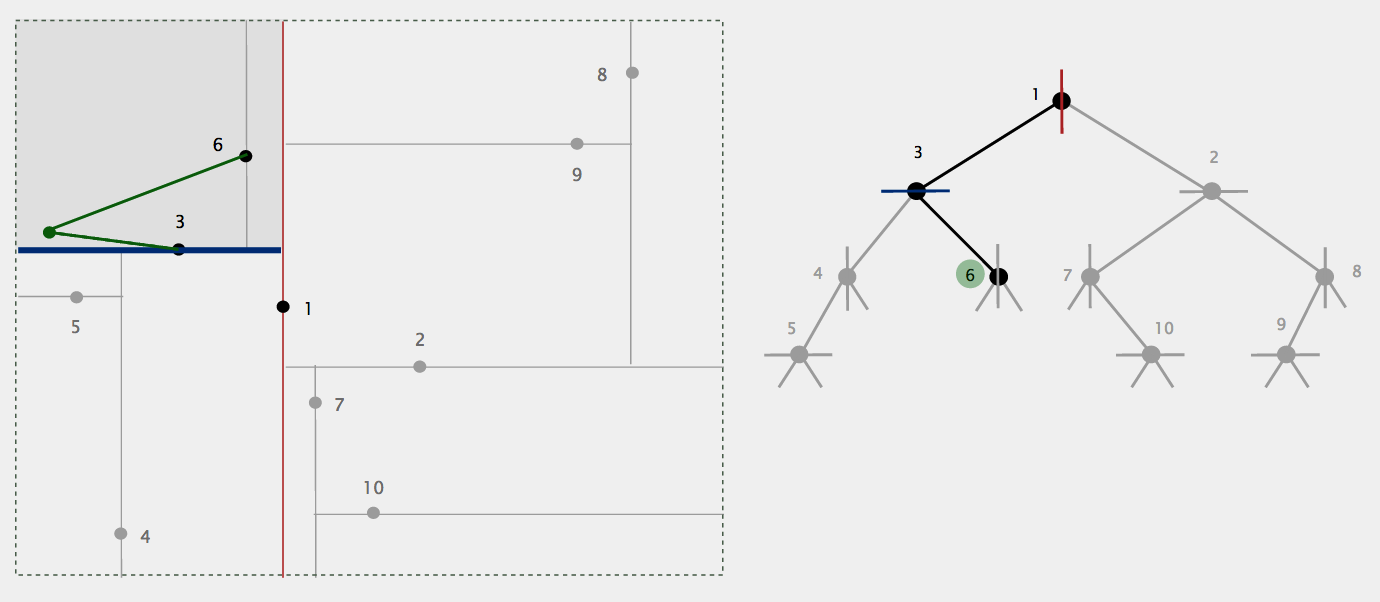
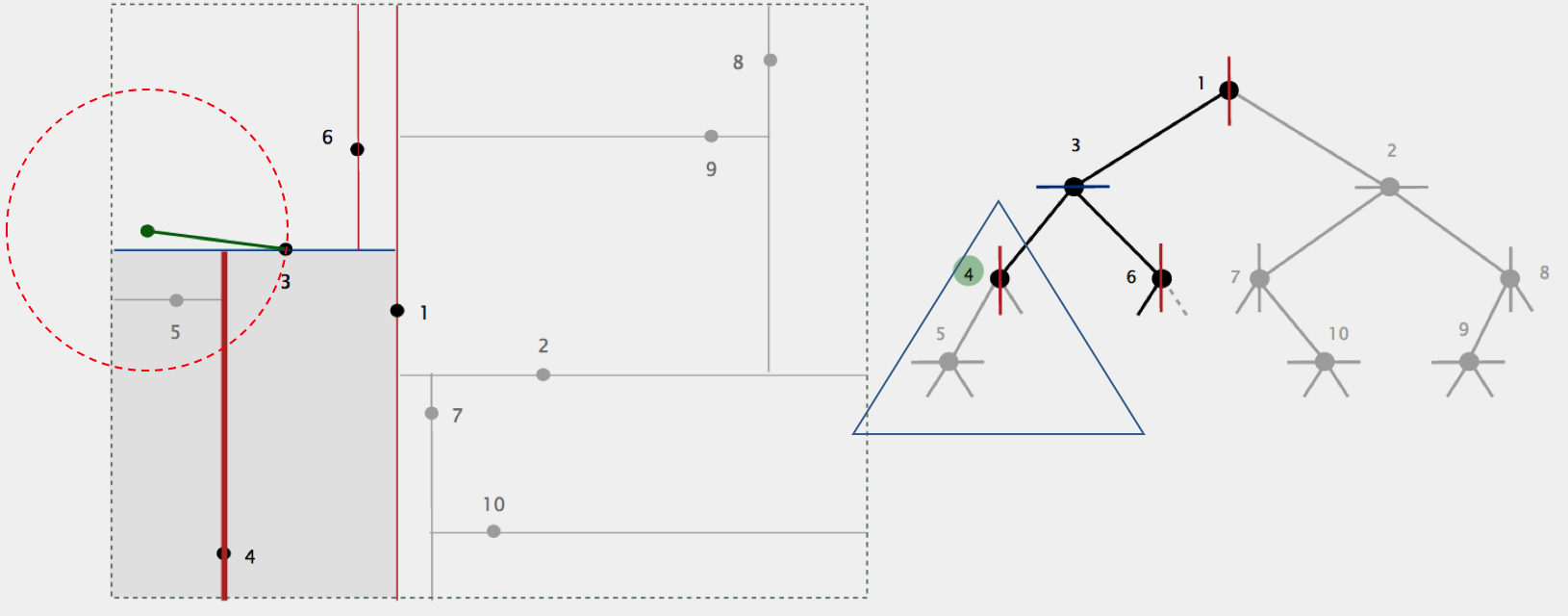
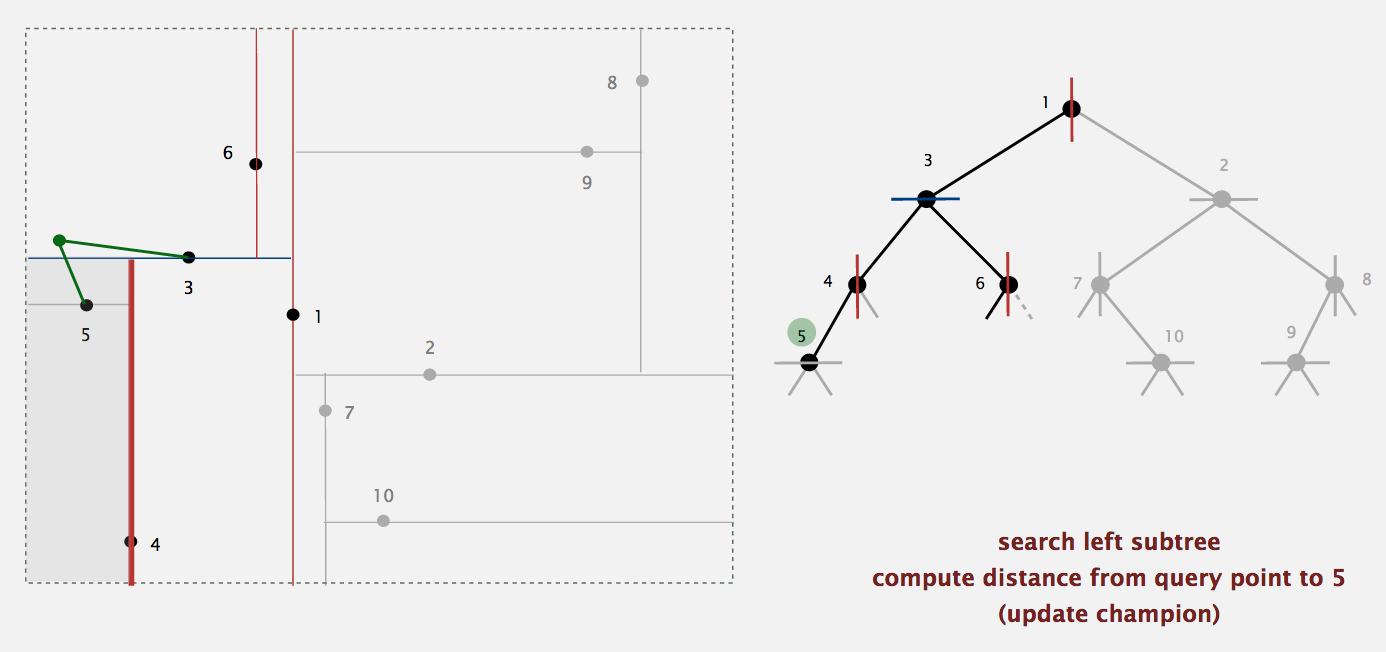
示例2：

维基百科上的一个动画例子（https://en.wikipedia.org/wiki/K-d_tree）

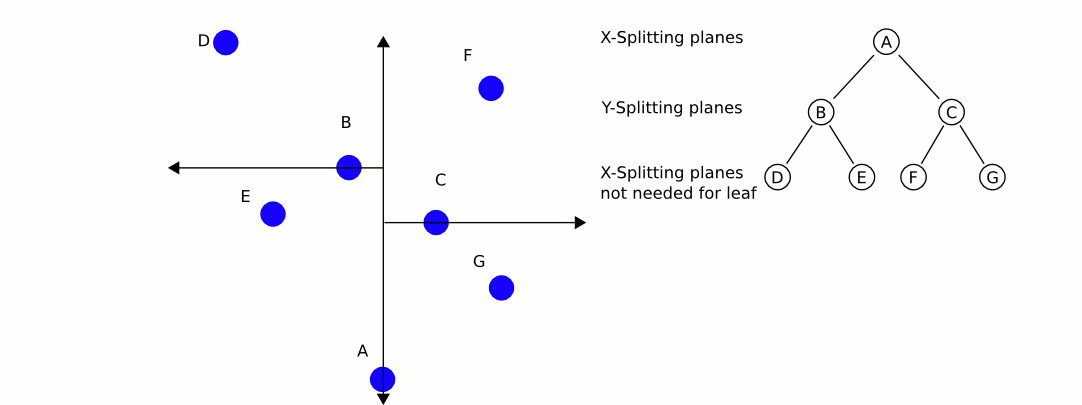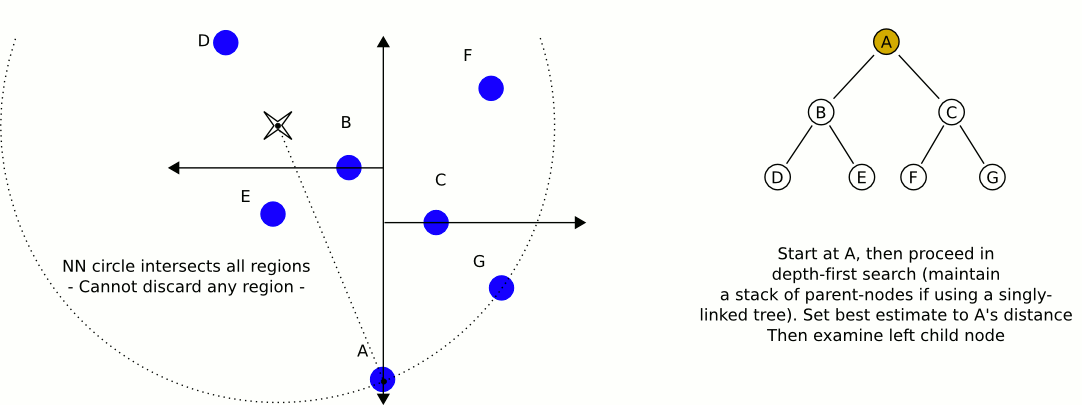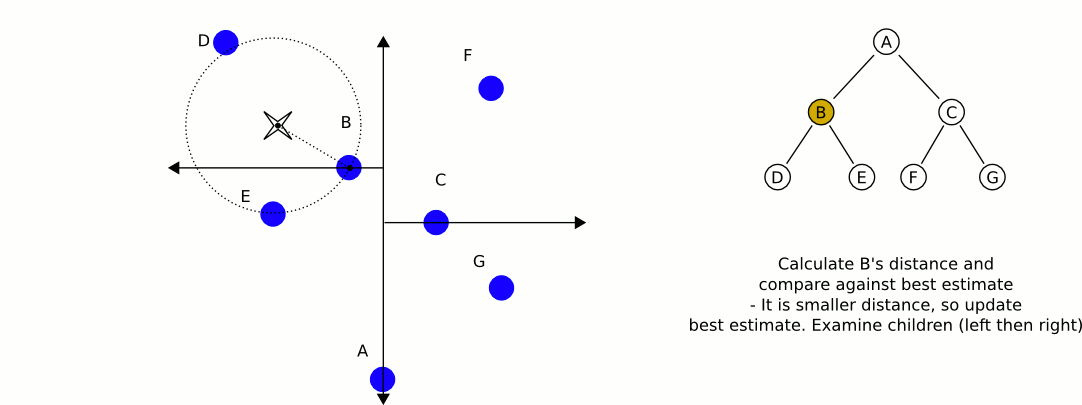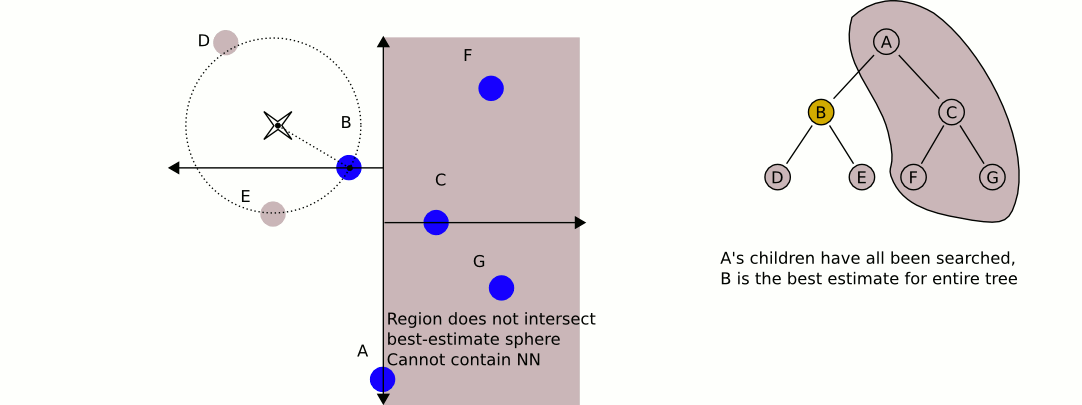
By User A1 at English Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=16242339