神经网络中符号的定义
我们首先给出网络中权重、偏置和激活值的符号定义。
我们用 l 来表示神经网络的层数,第一次层是输入的值,最后一层是输出的值。
权重:wjkl表示的是从(l−1)th层的第kth个神经元到lth层的第jth个神经元的链接上的权重。
偏置:bjl表示在lth层的第jth个神经元的偏置。
激活值的输入:zjl表示在第lth的第jth神经元激活值的输入。也就是
zjl=k∑wjklakl−1+bjl
激活值:ajl表示在lth层的第jth个神经元的激活值。也就是
ajl=σ(zjl)=σ(k∑wjklakl−1+bjl)
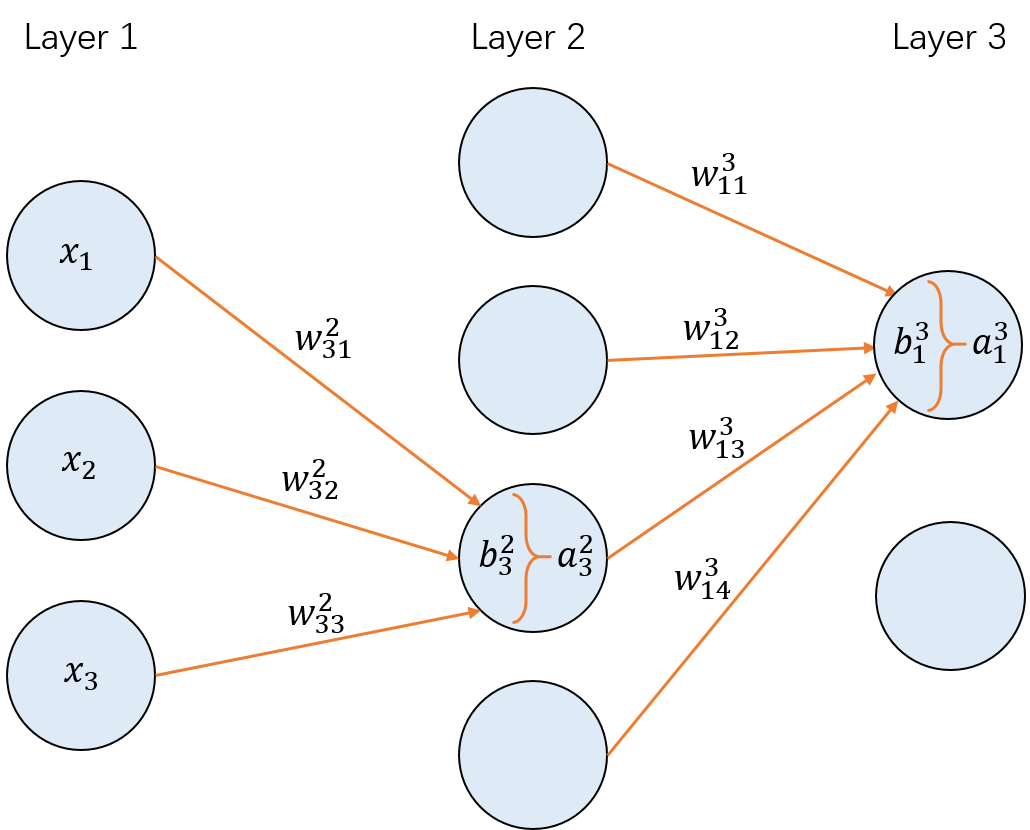
上面的图中 a32=σ(w312⋅x1+w322⋅x2+w332⋅x3+b32)。 也就是
ajl=σ(k∑wjkl⋅akl−1+bjl)=σ(wjl⋅al−1+bjl)
其求和是在第(l−1)th上的所有k个神经元上进行,其中wjl表示的是第(l−1)th层到第lth层的第j个神经元的权重向量。
我们先将每一层用矩阵表达,假定第(l−1)th有m个神经元,第lth层有n个神经元,那么从第(l−1)th到第lth层的权重个数有m×n个,偏置个数有n个。则:
第(l−1)th的神经元向量为al−1=⎣⎢⎢⎢⎢⎡a1l−1a2l−1a3l−1...aml−1⎦⎥⎥⎥⎥⎤,第lth层的神经元向量为al=⎣⎢⎢⎢⎢⎡a1la2la3l...anl⎦⎥⎥⎥⎥⎤,
偏置向量为bl=⎣⎢⎢⎢⎢⎡b1lb2lb3l...bnl⎦⎥⎥⎥⎥⎤,权重矩阵为:Wl=⎣⎢⎢⎢⎢⎡w11w21w31...wn1w12w22w12wn2w13w23w13wn3............w1mw1mw1mwnm⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡w1lw2lw3l...wnl⎦⎥⎥⎥⎥⎤
也就是:
al=⎣⎢⎢⎢⎢⎡a1la2la3l...anl⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡σ(w1l⋅al−1+b1l)σ(w2l⋅al−1+b2l)σ(w3l⋅al−1+b3l)...σ(wnl⋅al−1+bnl)⎦⎥⎥⎥⎥⎤
最后可以得到:
al=σ(Wl⋅al−1+bl)
这个表达式给出了一个更加全局的思考每层的激活值和前一层激活值的关联方式,我们仅仅用权重矩阵作用在激活值上,然后加上一个偏置向量,最后作用σ函数。
