Logistic分布
Logistic分布的定义:设X是连续随机变量,X服从Logistic分布是指具有下列分布函数和密度函数:
F(x)=P(X⩽x)=1+e−(x−μ)/γ1
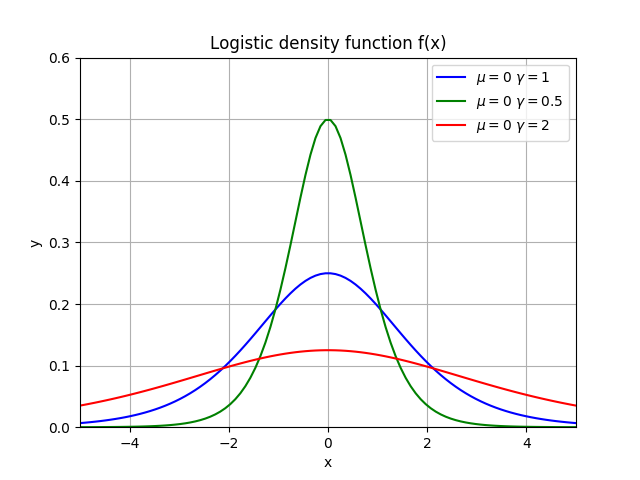
f(x)=F′(X⩽x)=γ(1+e−(x−μ)/γ)2e−(x−μ)/γ
其中,μ为位置参数,γ>0为形状参数。
概率分布函数如下(μ是位置函数,改变它可以平移图形):
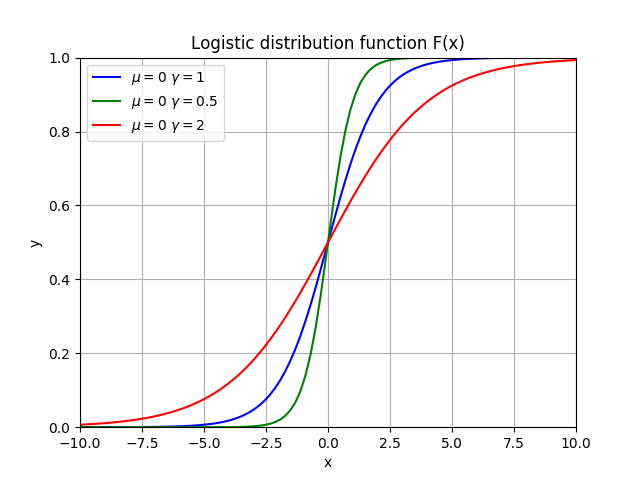
分布函数属于Logistic函数,是一条S形曲线(sigmoid curve)。该曲线以点(μ,21)为中心对称,即满足
F(−x+μ)−21=−F(x+μ)+21
曲线在中心附近增长速度比较快,两端增长速度比较慢。形状参数γ的值越小,曲线在中心附近增长的越快。
概率密度函数: