Logistic回归python实现

1.算法python代码

# -*- coding: utf-8 -*-

import matplotlib.pyplot as plt
import numpy as np

class Logistic(object):

    def __init__(self):
        self._history_w = []
        self._likelihood = []

    def load_input_data(self, data_file):
        with open(data_file) as f:
            input_x = []
            input_y = []
            for line in f:
                [x1, x2, y] = line.split()
                input_x.append([1.0, float(x1), float(x2)])
                input_y.append(int(y))
        self._input_x = np.array(input_x, dtype=np.float128)
        self._input_y = np.array(input_y, dtype=np.float128).T

    def sigmoid(self, x, w):                    # sigmoid函数
        return 1.0/(1+ np.exp(-np.inner(w,x)))

    def likelihood_function(self, w):           # 目标极大似然函数
        temp = np.inner(self._input_x, w)
        a = np.inner(temp.T, self._input_y)
        b = np.sum(np.log(1+np.exp(temp)))
        return b-a

    def batch_gradient_descent(self, iter_num, iter_rate): #批量梯度下降
        (data_num, features) = np.shape(self._input_x)
        w = np.ones(features)      #初始化w为全1向量
        for i in range(iter_num):
            theta = self.sigmoid(self._input_x, w)
            delta = theta - self._input_y
            w = w - iter_rate * np.inner(self._input_x.T, delta)  # 迭代更新w
            self._history_w.append(w)
            self._likelihood.append(self.likelihood_function(w))
        self._final_w = w
        return w

    def stochastic_gradient_descent(self, iter_num, iter_rate): #随机梯度下降
        (data_num, features) = np.shape(self._input_x)
        w = np.ones(features)  #初始化w为全1向量
        iter_range = range(iter_num)
        data_range = range(data_num)
        for i in range(iter_num):
            for j in data_range:
                iter_rate = 4/(1.0+j+i) + 0.01         # 学习率随着迭代的次数而不断变小
                theta = self.sigmoid(self._input_x[j], w)
                delta = theta - self._input_y[j]
                w = w - iter_rate * delta* self._input_x[j] # 迭代更新w
                self._history_w.append(w)
                self._likelihood.append(self.likelihood_function(w))
        self._final_w = w
        return w

2. python数据显示

在类中添加如下函数：

    def draw_result(self, title):
        total_data = np.shape(self._input_y)[0]
        self._nagtive_x = []
        self._positive_x = []
        for i in range(total_data):
            if self._input_y[i] > 0:
                self._positive_x.append(self._input_x[i])
            else:
                self._nagtive_x.append(self._input_x[i])

        plt.figure(1)
        x1 = [x[1] for x in self._positive_x]
        x2 = [x[2] for x in self._positive_x]
        plt.scatter(x1, x2, label='positive', color='g', s=20, marker="o") # 显示值为1的数据
        x1 = [x[1] for x in self._nagtive_x]
        x2 = [x[2] for x in self._nagtive_x]
        plt.scatter(x1, x2, label='nagtive', color='r', s=20, marker="x") # 显示值为0的数据
        plt.xlabel('x1')
        plt.ylabel('x2')
        def f(x):
            return -(self._final_w[0] + self._final_w[1]*x)/self._final_w[2]
        x = np.linspace(-4, 4, 10, endpoint=True)  # 显示学习到的直线
        plt.plot(x, f(x), 'b-', lw=1)
        plt.title(title)
        plt.legend()
        plt.show()

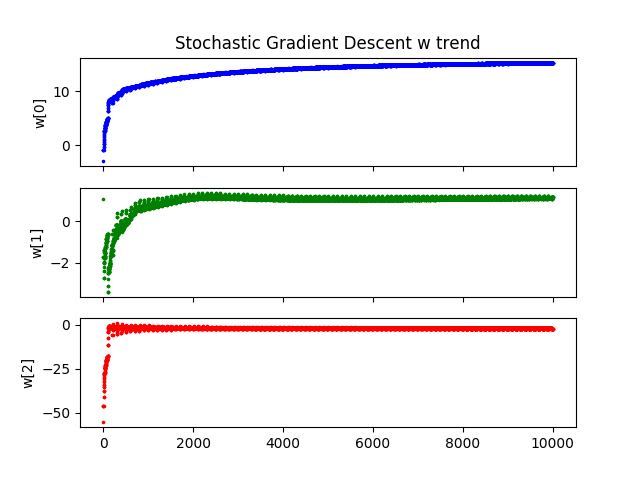
    def draw_w_history(self, title):
        f, (ax1, ax2, ax3) = plt.subplots(3, 1, sharex=True)
        x = np.arange(len(self._history_w))
        w0 = [w[0] for w in self._history_w]
        w1 = [w[1] for w in self._history_w]
        w2 = [w[2] for w in self._history_w]
        ax1.set_title(title+ ' w trend')
        ax1.set_ylabel('w[0]')
        ax1.scatter(x, w0, label='w[0]', color='b', s=10, marker=".")
        ax2.set_ylabel('w[1]')
        ax2.scatter(x, w1, label='w[1]', color='g', s=10, marker=".")
        ax3.set_ylabel('w[2]')
        ax3.scatter(x, w2, label='w[2]', color='r', s=10, marker=".")
        plt.show()

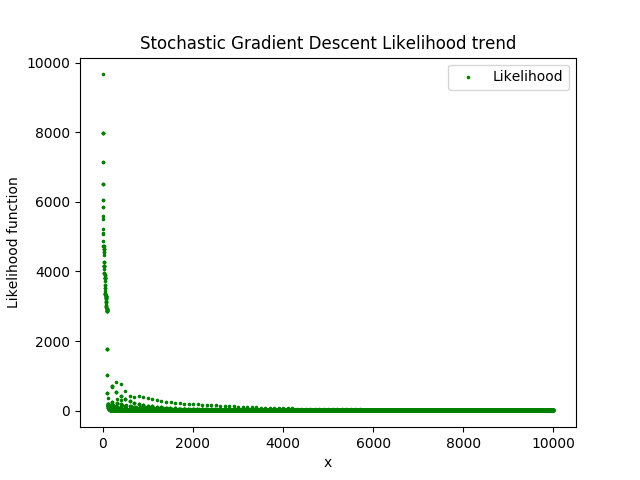
    def draw_likelihood_function(self, title):
        plt.figure(1)
        x = np.arange(len(self._likelihood))
        plt.scatter(x, self._likelihood, label='Likelihood', color='g', s=10, marker=".")
        plt.xlabel('x')
        plt.ylabel('Likelihood function')
        plt.title(title + ' Likelihood trend')
        plt.legend()
        plt.show()

3.数据集测试

数据集来自《机器学习实战》

https://github.com/apachecn/MachineLearning/blob/python-2.7/input/5.Logistic/TestSet.txt

3.1批量梯度下降

log = Logistic()
log.load_input_data("test.txt")
log.batch_gradient_descent(iter_num=300, iter_rate=0.001)
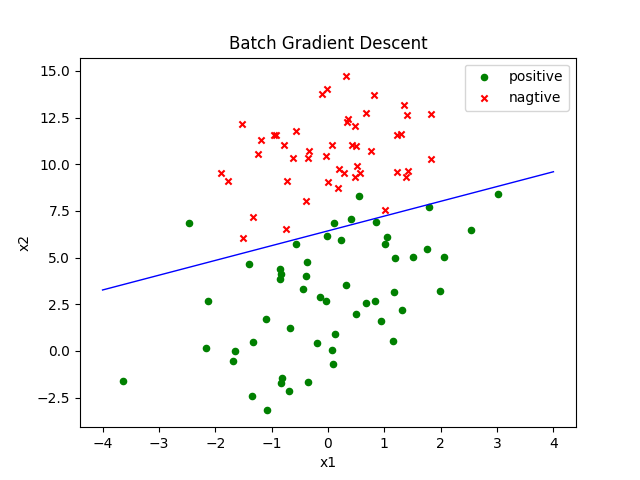
title = "Batch Gradient Descent"
log.draw_result(title)
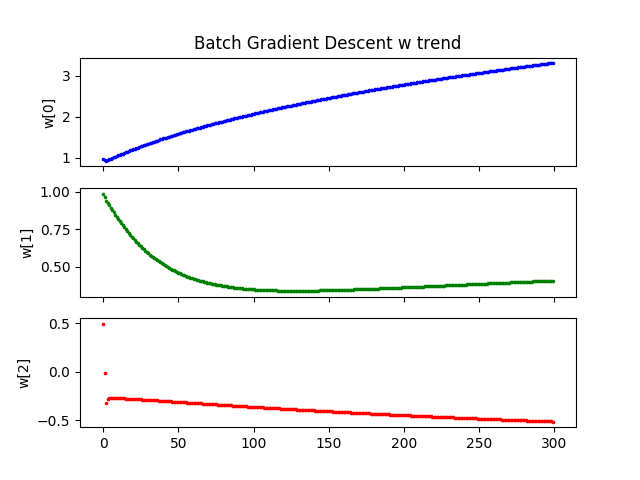
log.draw_w_history(title)
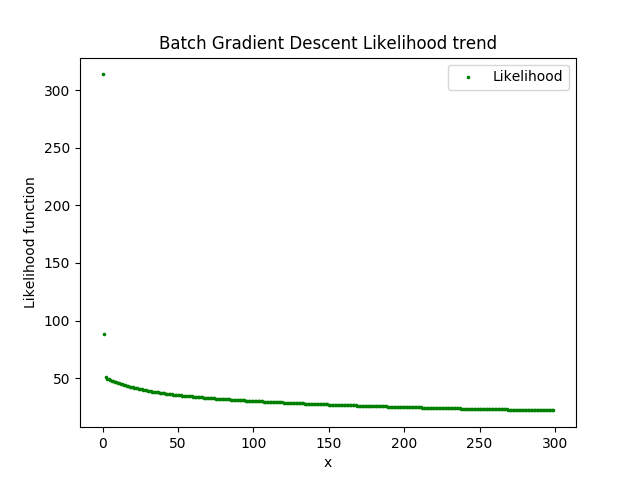
log.draw_likelihood_function(title)

总计算时间复杂度为300*100*3

3.2随机梯度下降

log = Logistic()
log.load_input_data("test.txt")
log.stochastic_gradient_descent(iter_num=100, iter_rate=0.001)
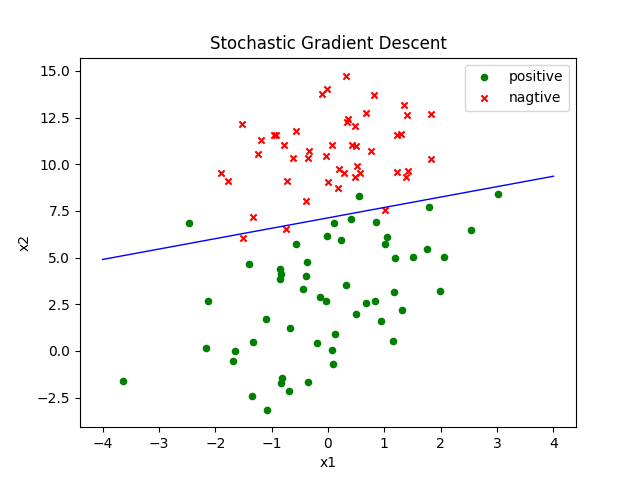
title = "Stochastic Gradient Descent"
log.draw_result(title)
log.draw_w_history(title)
log.draw_likelihood_function(title)

总计算时间复杂度为100（外循环）*100（内循环）*3

参考：

《机器学习实战》第五章