下面介绍反向传播基于的四个方程。
1. 输出层误差的方程
第L层为输出层,该层得分误差向量δL中每一个元素定义如下:
δjL=∂zjL∂C=∂ajL∂Cσ′(zjL)
右式第一项∂ajL∂C表示代价随着jth输出激活值的变化而变化的速度,第二项σ′(zjL)刻画了在zjL处激活函数σ的变化速度。
证明:应用链式法则我们可以就输出激活值的偏导数的形式重新表示上面的偏导数:
δjL=∂zjL∂C=k∑∂akL∂C∂zjL∂akL
这里的求和是在输出层的所有神经元上运行的,当k≠j时∂zjL∂akL=0,于是,我们可以简化方程为:
δjL=∂ajL∂C∂zjL∂ajL
然后ajL=σ(zjL),于是,可以写成
δjL=∂ajL∂Cσ′(zjL)
以矩阵的形式重写方程,其中每个元素∂ajL∂C构成的向量表示成∇aC,每个元素σ′(zjL)构成的向量表示成σ′(zL),于是得到
δL=⎣⎢⎢⎢⎢⎡δ1Lδ2Lδ3L...δnL⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡∂a1L∂Cσ′(z1L)∂a2L∂Cσ′(z2L)∂a3L∂Cσ′(z3L)...∂anL∂Cσ′(znL)⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤=∇aC⊙σ′(zL)
2. 使用下一层的误差δl+1来表示当前层误差δl
特别的,
δl=((wl+1)Tδl+1)⊙σ′(zl)
其中(wl+1)T是(l+1)th层权重矩阵wl+1的转置。这个公式看过去有点复杂,但是每个元素都有很好得分解释,假设我们知道(l+1)th的误差向量δl+1,当我们应用转置的权重矩阵(wl+1)T,我们可以把它看做是沿着网络反向移动误差,给了我们度量在lth层的误差的方法。然后进行Hadamard乘积运算σ′(zl),这会让误差通过l层的激活函数反向传递回来并给出在第l层的带权输入误差向量δl。
根据该公式,我们可以首先根据第一个公式得到输出层的误差δL,然后得到第(L−1)th层的误差,如此一步步地方向传播完整个网络。
证明:根据链式法则,我们可以将δjl=∂zjl∂C写成:
δjl=∂zjl∂C=k∑∂zkl+1∂C∂zjl∂zkl+1=k∑∂zjl∂zkl+1δkl+1
这里我们将最后一个式子交换了两边的项,并用δkl+1代入。然后
zkl+1=j∑wkjl+1ajl+bkl+1=j∑wkjl+1σ(zjl)+bkl+1
做微分,我们得到
∂zjl∂zkl+1=wkjl+1σ′(zjl)
代入上式,得到
δjl=k∑wkjl+1σ′(zjl)δkl+1=(k∑wkjl+1δkl+1)σ′(zjl)
将公式进行矩阵化,最后得到第一个公式。
举例来说,如下图:
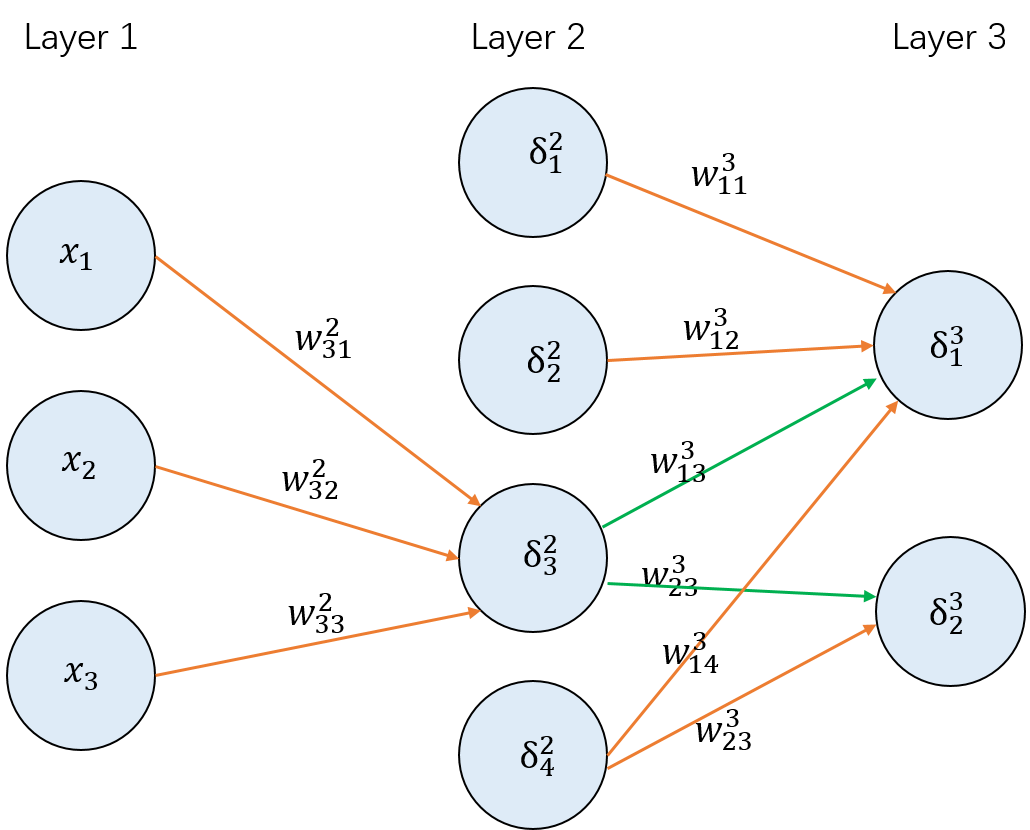
当我们已经计算得到了第3层的误差向量δ3=[δ13δ23],这时计算第2层的误差向量δ2,我们先计算δ32,根据上面的公式可以得到
δ32=(k∑wk33δk3)σ′(z33)=(w133δ13+w233δ23)σ′(z32)=([w133w233]T⋅[δ13δ23])σ′(z32)
也就是图中两条绿色的线所标识的权重与误差的乘积和。
3. 代价函数关于网络中任意偏置的改变率
∂bjl∂C=δjl
也就是误差δjl和∂bjl∂C完全一致。
证明:根据链式法则,其中zjl=k∑wjklakl−1+bjl,最终可以得到
∂bjl∂C=∂zjl∂C∂bjl∂zjl=∂zjl∂C
用矩阵表示,可以表示成:
∂bl∂C=δl
4. 代价函数关于任何一个权重的改变率
∂wjkl∂C=akl−1δjl
证明:根据链式法则,其中zjl=k∑wjklakl−1+bjl,最终可以得到
∂wjkl∂C=∂zjl∂C∂bjl∂zjl=∂zjl∂Cajl−1=akl−1δjl
举例来说:
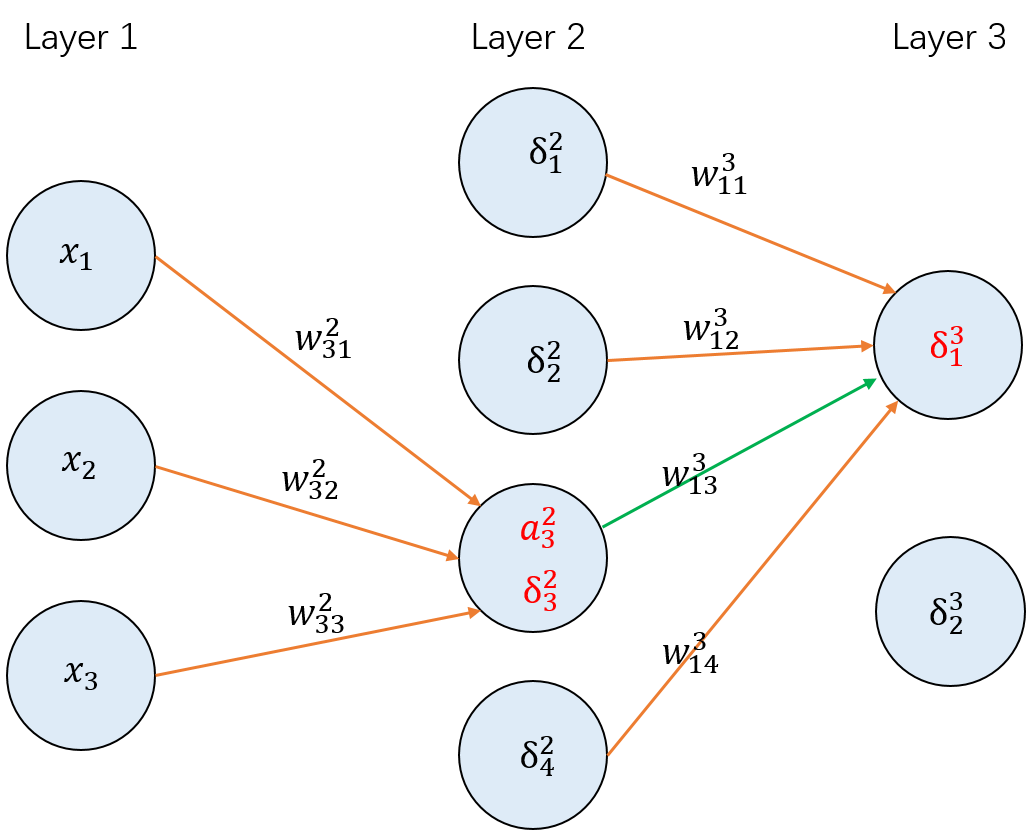
上面图中,想要计算∂w133∂C,则∂w133∂C=a32δ13。也可以理解成:
∂w∂C=ainδout
其中ain是输入给权重w的神经元的激活值,δout是输出自权重w的神经元的误差。
用矩阵表示,可以表示成(其中第(l−1)th层神经元有m个,第lth层神经元有n个)
∂wl∂C=∂C/∂⎣⎢⎢⎢⎢⎡w11lw21lw31l...wn1lw12lw22lw12lwn2lw13lw23lw13lwn3l............w1mlw1mlw1mlwnml⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡a1l−1δ1la1l−1δ2la1l−1δ3l...a1l−1δnla2l−1δ1la2l−1δ2la2l−1δ3la2l−1δnla3l−1δ1la3l−1δ2la3l−1δ3la3l−1δnl............aml−1δ1laml−1δ2laml−1δ3laml−1δnl⎦⎥⎥⎥⎥⎤
于是得到:
∂wl∂C=⎣⎢⎢⎢⎢⎡δ1lδ2lδ3l...δnl⎦⎥⎥⎥⎥⎤⋅[a1l−1,a2l−1,...,aml−1]
其中[δ1l,δ2l,...,δnl]是n∗1,[a1l−1,a2l−1,...,aml−1]是1∗m,最终得到n∗m的权重矩阵。

